While the allure of correlations might offer apparent connections between variables, it often conceals the pitfalls of spurious relationships—mere statistical coincidences devoid of causal underpinnings. As businesses delve into vast datasets seeking insights into the factors influencing their bottom line there’s a pressing need to navigate beyond correlations that may deceive rather than enlighten. For instance, CFOs overseeing sizable corporations must discern the variables influencing specific revenue and cost components to establish precise financial forecasts. Furthermore, as articulated by esteemed computer scientist Judea Pearl, the solitary pursuit of data analysis does not suffice to address causal intricacies and necessitates the incorporation of contextual considerations. This article aims to unravel the intricate interplay between correlations and causations where in the realm of AI in finance, discerning between these two concepts becomes paramount for unlocking genuine predictive relationships that drive business outcomes.
Correlation is not causation, but it sure is a hint. - Judea Pearl
Correlation
Correlation is a statistical measure that quantifies the degree of association or relationship between two variables, such as revenue and the number of visitors or operating expenses and inflation. It provides insights into how changes in one variable relate to changes in another. Positively correlated variables simultaneously increase or decrease, while negatively correlated variables experience inverse variations. Alternatively, a lack of any observable pattern denotes a non-correlational relationship.
The value of correlations lies in their ability to indicate a predictive relationship. Suppose being assigned the responsibility of predicting the operational expenses associated with utility costs for your corporate entity and that the predominant contributor is the cost of heating. Therefore, these costs decrease on warmer days, exploiting the correlation observed between temperature and utility costs. It is imperative to underscore that correlation denotes a bidirectional association without any inherent directionality. Employing the aforementioned example, rising temperatures lead to lowering utility costs, while conversely, augmented utility costs lead to heightened temperatures. Nevertheless, it is evident that the manipulation of temperature cannot be achieved through incurring a specified amount of utility costs.
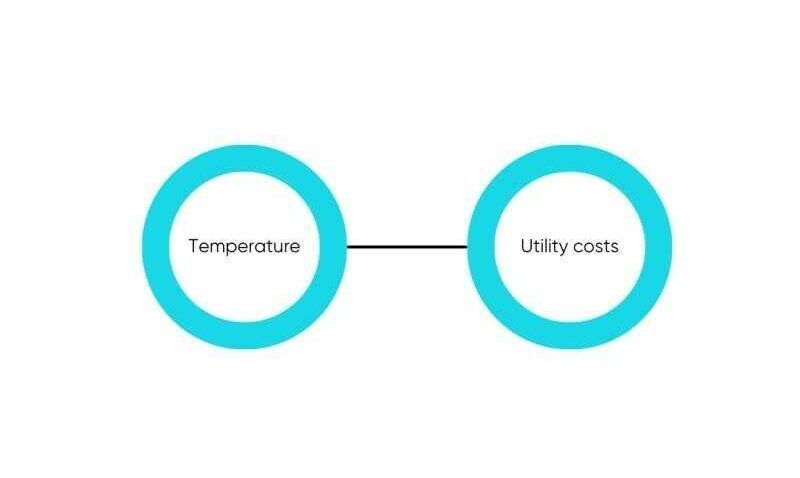
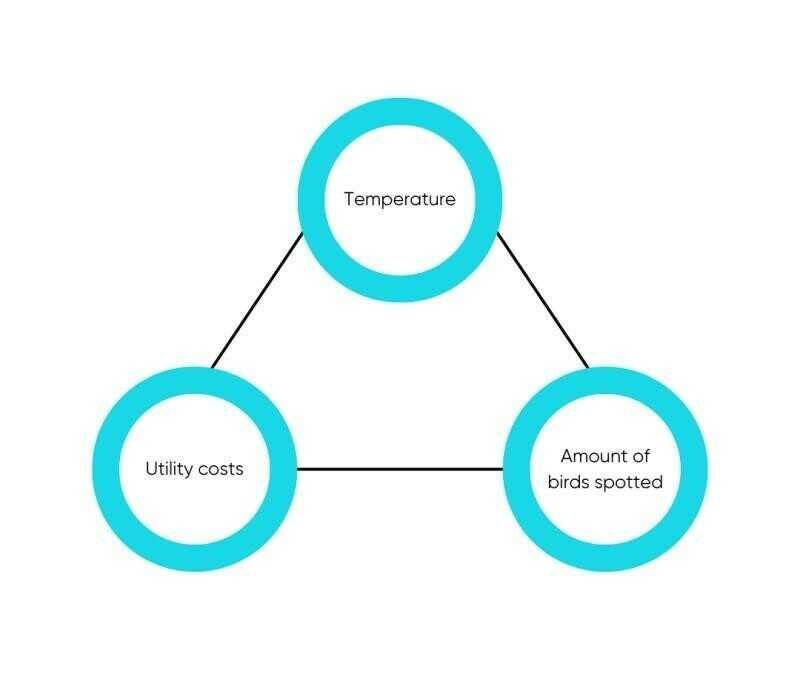
By modelling relationships between variables solely based on data-driven approaches such as correlations, the inevitability of encountering spurious correlations arises due to the absence of intrinsic cause-and-effect connections. Within these instances, the apparent association is coincidental, stemming from the influence of a third variable, commonly denoted as a confounder, which impacts both variables. To illustrate, the substantial correlation between the number of birds observed and the utility costs does not denote a causal relationship. Rather, the confounding variable—in this instance, temperature—exerts an influence on both the utility costs and the frequency of bird sightings, thereby creating a spurious correlation.
Causation
Causation indicates a cause-and-effect relationship between two variables. It implies that changes in one variable directly influence changes in the other. For instance, rising kerosene prices will cause higher costs for companies maintaining a fleet of cargo planes, a consequence not applicable to enterprises managing a fleet of electric taxis. Establishing the presence of a causal relationship requires specific criteria, several of which are delineated below:
- Association: The existence of correlation between the cause and its effect. It is trivial that if no (lagged) correlation exists between two variables such as the price of kerosene and the expenditures of a company maintaining a fleet of cargo planes, no causal relationship can exist.
- Temporal Order: The cause must chronologically precede the effect, establishing a clear temporal sequence. For instance, rising unemployment rates will cause a decline in inflation and not the other way around,
- Non-Spuriousness: Ensuring that the observed relationship is not an artefact resulting from the influence of a confounding variable, such as the temperature on the utility costs and the amount of bird sightings.
- Context: Acknowledging that the cause-and-effect relationship is contingent upon the contextual conditions in which it manifests. For instance, the temperature variable needs to denote the temperature from the location of the facilities requiring heating.
Causations prove beneficial due to their capacity to signify genuine predictive relationships, while preventing the presence of spurious relationships and adding a discernible sense of direction given a specified context.
Consider the example where utility costs, temperatures and the amount of spotted birds exhibit correlation. Intuitively, it becomes evident that temperature serves as both a driving force for utility costs and for the amount of bird sightings. In the schematic representation, arrows denote causal relationships, specifically originating from the temperature variable and extending towards the other variables. No arrows are connecting the amount of birds and the utility costs, meaning that future utility costs should not be modelled based on future bird sightings.
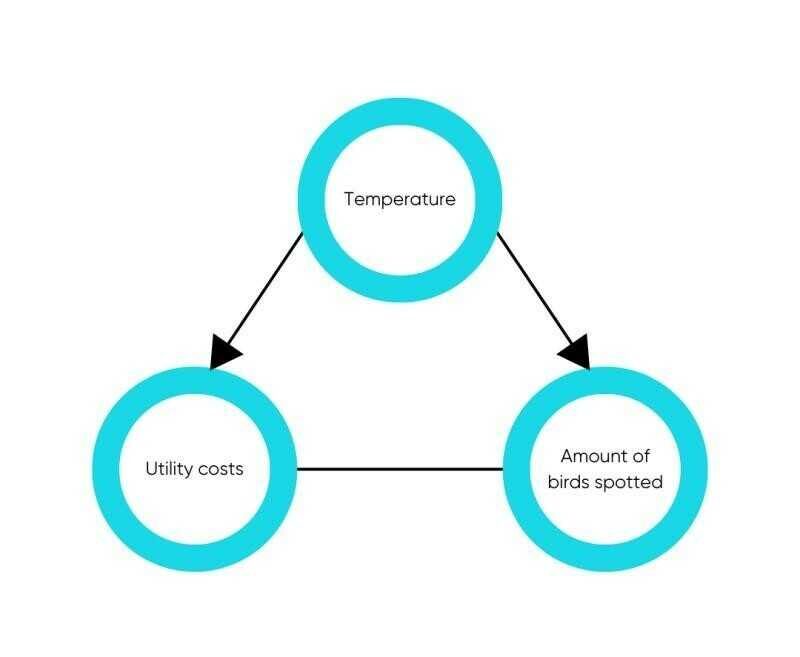
The key insight from this examination is that context is essential for determining genuine predictive relationships. The clarity of this contextual relevance may vary. Therefore, models that effectively incorporate such contextual nuances require extending beyond data-driven methodologies alone.
The importance for Finance teams
As a CFO overseeing a sizeable corporation and having to discern the variables influencing specific revenue and cost components to establish precise financial forecasts, initial steps involve computing correlations among all pairs of variables, followed by a meticulous examination to ascertain causations. Although there exist instances where causal relationships are not readily derivable from the provided context and demand a manual examination, going through thousands of correlations does not provide a scalable methodology to find genuine predictive relationships. Therefore, automatically determining causal relationships between variables becomes inevitable.
A well-known methodology exists called Granger causality. However, this test does not necessarily test true causality, but rather a temporal relation, as it is still possible that both variables are driven by a confounding variable. Moreover, as per Judea Pearl, it does not incorporate any form of context.
Predikt, in its endeavours, embarked on the quest for novel methodologies using generative AI to provide automated causality among extensive sets of variable pairs. Notably, the suitability of large language models for this endeavour was identified, given their inherent capacity to encapsulate latent real-world knowledge and engage in context-specific reasoning to delineate sound causal relationships among variables. Consequently, comprehensive and robust predictive analytics models can be provided to companies looking to grasp a thorough understanding of what variables impact their business. By incorporating external macroeconomic variables, Predikt is able to create a complete digital twin, providing superior insights and a thorough understanding of the effect of market signals on their business.
Conclusion
Exposing genuine predictive relationships by connecting variables that correlate as well as causate is an essential part of any AI tool. Only then can issues arising from confounding variables and mere coincidences be omitted, resulting in robust and trustworthy predictive models that can autonomously discern causating variables from contextual cues. Essential components that form the foundation for comprehensive and impactful predictive analytics models provided by Predikt. Allowing for the creation of a digital twin capable of providing superior insights and state of the art forecasts for financial planning.